GRPO with Verifiable (Binary) Rewards Is an Adaptive Weighted Contrastive Loss

1. Grouped Reward Policy Optimization

The goal of this short blog is to understand GRPO that was used successfully to train Deepseek models. We will limit our analysis to binary rewards or what Tulu authors calls RLVR (Reinforcement learning with Verifiable Rewards.)

Understanding GRPO with Rule Based (Binary) Reward

GRPO has been successfully used in DeepSeek (v3,math, and R1) especially with rule based rewards (verifiable rewards, i.e binary rewards), the goal of this note is to understand it. GRPO optimizes the following objective:

$$\underset{\theta }{max}{\mathbb{E}}_q{\mathbb{E}}_{o\sim {\pi }_{{\theta }_{\text{old}}}(.|q)}f(\frac{{\pi }_{\theta }(o|q)}{{\pi }_{{\theta }_{\text{old}}}(o|q)},A(o))-\beta \mathrm{KL}({\pi }_{\theta }||{\pi }_{\mathrm{ref}})$$

Where the advantage function $A(o)$ is defined as follows :

$$A(o)=\frac{r(o)-\mu }{\sigma }$$

where $\mu =E_{o\sim {\pi }_{{\theta }_{\text{old}}}(.|q)}r(o)$ and $\sigma =\sqrt{V_{o\sim {\pi }_{{\theta }_{\text{old}}(.|q)}}r(o)}$.

And

$$f(x,y)=min(xy,\text{clip}(x,1-\epsilon ,1+\epsilon )y)$$

Note that in our context $x=\frac{{\pi }_{\theta }(o|q)}{{\pi }_{{\theta }_{\text{old}}}(o|q)}>0$ and the advantage $A(o)$ can be positive or negative and hence if $A(o)>0$ we have :

$$f(\frac{{\pi }_{\theta }(o|q)}{{\pi }_{{\theta }_{\text{old}}}(o|q)},A(o))=A(o)min(\frac{{\pi }_{\theta }(o|q)}{{\pi }_{{\theta }_{\text{old}}}(o|q)},1+\epsilon )$$

and if $A(o)<0$

$$f(\frac{{\pi }_{\theta }(o|q)}{{\pi }_{{\theta }_{\text{old}}}(o|q)},A(o))=A(o)max(\frac{{\pi }_{\theta }(o|q)}{{\pi }_{{\theta }_{\text{old}}}(o|q)},1-\epsilon )$$

We will assume that we have a rule based reward that evaluates correctness of a reasoning or the execution of the code meaning that $r(o)\in 0,1$. We note : $$p:=p_{{\theta }_{\text{old}}}(q)={\mathbb{P}}_{o\sim {\pi }_{{\theta }_{\text{old}}}}(r(o)=1)\text{probability of success}$$ Hence we have for mean and variance of a Bernoulli random variable :$\mu =p$ and $\sigma =p(1-p)$. We assume here $0<p<1$ to not to have to deal with singularities. Hence replacing mean and variance in the advantage function:

$$A(o)=\{\begin{array}{lll}\frac{1-p}{\sqrt{p(1-p)}}& \text{if }r(o)=1,-\frac{p}{\sqrt{p(1-p)}}& \text{if }r(o)=0.\end{array}$$

which simplifies to : $$A(o)=\{\begin{array}{lll}\sqrt{\frac{1-p}{p}}& \text{if }r(o)=1,-\sqrt{\frac{p}{(1-p)}}& \text{if }r(o)=0.\end{array}$$

Hence we have:

$$E_{o\sim {\pi }_{{\theta }_{\text{old}}(.|q)}}f(\frac{{\pi }_{\theta }(o|q)}{{\pi }_{{\theta }_{\text{old}}}(o|q)},A(o))=$$

$$\sqrt{\frac{1-p}{p}}{E}_{o\sim {\pi }_{{\theta }_{\text{old}}}(.|q)}min(\frac{{\pi }_{\theta }(o|q)}{{\pi }_{{\theta }_{\text{old}}}(o|q)},1+\epsilon )1_{r(o)=1}$$

$$-\sqrt{\frac{p}{(1-p)}}{E}_{o\sim {\pi }_{{\theta }_{\text{old}}}(.|q)}max(\frac{{\pi }_{\theta }(o|q)}{{\pi }_{{\theta }_{\text{old}}}(o|q)},1-\epsilon )1_{r(o)=0}$$

and hence the overall cost is obtained by taking expectation over $q$, note that $p=p_{{\theta }_{\text{old}}}(q)$:

$$E_q\sqrt{\frac{1-p_{{\theta }_{\text{old}}}(q)}{p_{{\theta }_{\text{old}}}(q)}}{E}_{o\sim {\pi }_{{\theta }_{\text{old}}}(.|q)}min(\frac{{\pi }_{\theta }(o|q)}{{\pi }_{{\theta }_{\text{old}}}(o|q)},1+\epsilon )1_{r(o)=1}$$

$$-E_q\sqrt{\frac{p_{{\theta }_{\text{old}}}(q)}{(1-p_{{\theta }_{\text{old}}}(q))}}{E}_{o\sim {\pi }_{{\theta }_{\text{old}}}(.|q)}max(\frac{{\pi }_{\theta }(o|q)}{{\pi }_{{\theta }_{\text{old}}}(o|q)},1-\epsilon )1_{r(o)=0}$$

$$-\beta \mathrm{KL}({\pi }_{\theta }||{\pi }_{\mathrm{ref}})$$

full derivation available here

Loss Interpretation

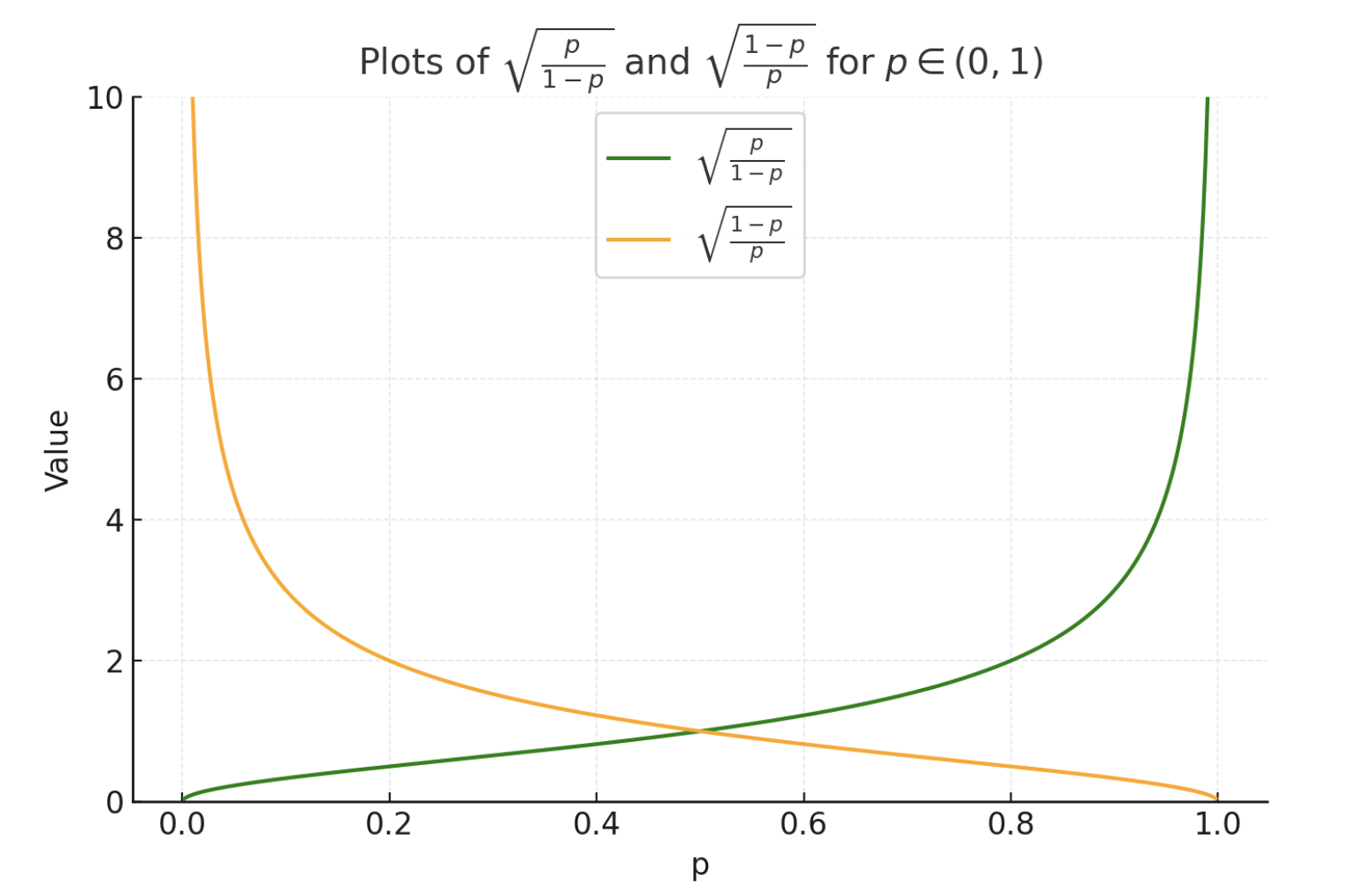
We see that GRPO is effectively a weighted contrastive loss that is weighted by a ratio depending on the probability of success of the old policy (p):

We see from the weights plots that :

• if the success probability of old policy is high (say p >0.5), the weighting for points with success is low since the old policy is already good, and for failing point the weight is high and hence they are more penalized
• If the success probability of old policy is low (say p <0.5), the weighting for points with success is high since we want to reinforce those successes, and for failing points these are still penalized but with a small weight

More observations due to clipping:

• for correct outputs the cost is constant $(1+\epsilon )$ if ${\pi }_{\theta }(o|q)\ge (1+\epsilon ){\pi }_{{\theta }_{\text{old}}}(o|q)$
• for wrong outputs the cost is $(1-\epsilon )$ if ${\pi }_{\theta }(o|q)\le (1-\epsilon ){\pi }_{{\theta }_{\text{old}}}(o|q)$,

2 Conclusion

In summary, the standardized reward or the advantage function used in GRPO results in an interesting adaptive weighted contrastive loss : if the probability of success of the old policy is high, the wrong answers are more penalized than the correct ones are reinforced. If the probability of success of old policy is low , the correct answers are more reinforced than the wrong answers are penalized.

References

• Guo, Daya, et al. “Deepseek-r1: Incentivizing reasoning capability in llms via reinforcement learning.” arXiv preprint arXiv:2501.12948 (2025).
• Shao, Zhihong, et al. “Deepseekmath: Pushing the limits of mathematical reasoning in open language models.” arXiv preprint arXiv:2402.03300 (2024).
• Lambert, Nathan, et al. “TULU 3: Pushing Frontiers in Open Language Model Post-Training.” arXiv preprint arXiv:2411.15124 (2024).