GRPO Amplifies the Success Rate of A Policy via An implicit Fixed Point Iteration

In the previous post, we established that GRPO with verifiable rewards can be seen as a weighted contastive policy optimization, where positive and negative samples are synthetic data sampled from the old policy and labeled via the verifiable reward. In this post we will review our recent preprint that builds on this observation and analyses the dynamics of GRPO and the probability of success of the verifiable reward under GRPO’s optimized policy.

1 GRPO’s Success Rate Recursion

GRPO with no Clipping Equivalent Contrastive Loss formulation

For $\epsilon >0$, and for $p\in [0,1]$ define the following weights:

$${\omega }_{+,\epsilon }(p)=\frac{1-p}{\sqrt{p(1-p)+\epsilon }}$$ $${\omega }_{-,\epsilon }(p)=\frac{p}{\sqrt{p(1-p)+\epsilon }}$$

Let ${\pi }_{{\theta }_{\text{old}}}$ be the old policy and let $p_{{\theta }_{\text{old}}}(q)$ be the probability of success of the verifiable reward $r$ under ${\pi }_{{\theta }_{\text{old}}}$ for a given prompt $q$: $$p_{{\theta }_{\text{old}}}(q)={\mathbb{E}}_{o\sim {\pi }_{{\theta }_{\text{old}}}(.|q)}{1}_{r(q,o)=1}$$

We can write GRPO with no clipping as the following contrastive optimization:

$$\underset{\theta }{max}L(\theta ),$$

where $L(\theta )=$

$$E_q{\omega }_{+,\epsilon }(p_{{\theta }_{\text{old}}}(q))E_{o\sim {\pi }_{\theta (.|q)}}{1}_{r(q,o)=1}-E_q{\omega }_{-,\epsilon }(p_{{\theta }_{\text{old}}}(q))E_{o\sim {\pi }_{\theta (.|q)}}{1}_{r(q,o)=0}$$ $$-\beta \mathrm{KL}({\pi }_{\theta }||{\pi }_{\mathrm{ref}}).$$

GRPO Iterations and Optimal Policy

We drop now the optimization on the parameter space and optimize on the space of policies hence GRPO iterations can be written follows for $n\ge 1$:

$${\pi }_n=arg\underset{\pi }{max}{L}_{n-1}(\pi )$$ where $L_{n-1}(\pi )=$ $${\mathbb{E}}_q({\omega }_{+,\epsilon }(p_{n-1}(q)){\mathbb{E}}_{o\sim \pi (.|q)}{1}_{r(q,o)=1}-{\omega }_{-,\epsilon }(p_{n-1}(q)){\mathbb{E}}_{o\sim \pi (.|q)}{1}_{r(q,o)=0})$$ $$-\beta \mathrm{KL}(\pi ||{\pi }_{\mathrm{ref}}),$$

and $p_{n-1}(q)$ is the probability of success of the policy ${\pi }_{n-1}(\cdot |q)$ and ${\pi }_0={\pi }_{\mathrm{ref}}$.

The optimal policy for $n\ge 1$ can be derived as follows:

GRPO’s Probability of Success Recursion

Computing now the success rate $p_n(q)$ of the policy ${\pi }_n(\cdot |q)$, and noting $p_{\mathrm{ref}}(q)$ the success rate of ${\pi }_{\mathrm{ref}}(\cdot |q)$, we obtain the following recursion:

$$p_n(q)=h_{\epsilon ,p_{\mathrm{ref}}(q)}(p_{n-1}(q)),$$

where $$h_{\epsilon ,p_{\mathrm{ref}}}(p)=\frac{1}{1+\frac{1-p_{\mathrm{ref}}}{p_{\mathrm{ref}}}\exp (-\frac{1}{\beta }\frac{1}{\sqrt{p(1-p)+\epsilon }})}$$

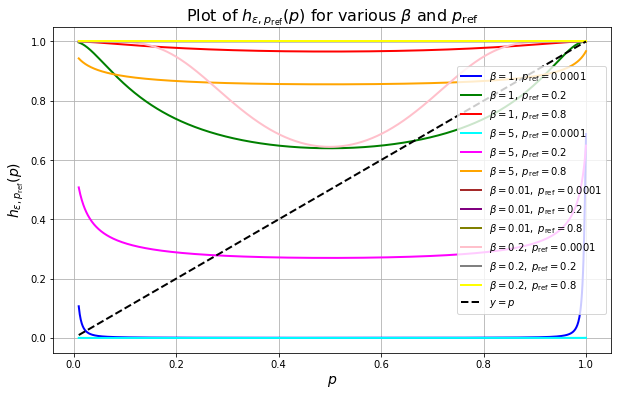
2 GRPO Amplifies Success Rate via An Implicit Fixed Point Iteration

We see that the success rate satisfies a fixed point iterations and the limit of this recursion as $n\to \mathrm{\infty }$ for each prompt $q$, $p^{\ast }(q)$ (the point in the curves above intersecting the function $h_{\epsilon ,p_{\mathrm{ref}}}$ and the line $y=p$). We show in the paper that under mild conditions on $\beta$:

• the sequence $p_n(q)$ converges locally to the the fixed point $p^{\ast }(q)$
• the fixed point success rate $p^{\ast }(q)$ is guaranteed to be larger then the reference success rate $p_{\mathrm{ref}}(q)$: $p^{\ast }(q)>p_{\mathrm{ref}}(q)$.

3 Conclusion

In summary, GRPO with verifiable rewards iterations leads to a fixed point iteration on the success rate of the policy. Under mild conditions, the limit success rate is guaranteed to amplify the success rate of the reference model and the local convergence of the iterates to the limit point is also guaranteed.